
Interseasonal Storage
We have already established that a relatively small solar PV installation can provide all the household electricity requirements during summer as long as it is supplemented with a big battery. If I can make the wind turbine work we will have a significant excess of electricity.As geographical latitude increases, the mismatch between power generation and power usage becomes more extreme. Space heating in winter introduces a large demand just when solar irradiance is at a minimum. The yield from wind power in the UK appears higher in winter, but it suffers from extended periods of lull which can last weeks typically in January or February the time of highest space heating demand. Wind energy seems at a maximum around the equinoxes, possibly because this is the greatest rate of change in earth surface temperature.
So the problem is how to store energy harvested in summer and during high wind turbine output to help heat the house in winter. Ideally the storage medium needs to be stable and not require special containment; this is why 'dirty' coal is so attractive ... just pile it up and burn it when needed.
Why is coal bad?
Let us start with "man-made atmospheric CO2 is adversely changing our climate". If you don't believe the overwhelming scientific evidence for this statement or recognise that burning fossil fuels has caused a significant increase in atmospheric CO2 then this place is probably not for you.Anthracite coal is more then 90% carbon; burning one tonne of coal produces about 2.85 tonnes of CO2 because oxygen is added during combustion. Other fossil fuels like natural gas (predominantly methane) produce less CO2 for an equivalent heat release. This is because some of the stored chemical energy in methane (CH4) is locked in bonds of the four hydrogen atoms which react to form harmless water (H2O). Methane still has one carbon atom so still produces CO2, so while methane is better than coal it is still releasing CO2 into the atmosphere.
Figures for CO2 emissions per kWh of delivered heat are difficult to find, but multiple sources suggest about 0.37kgCO2/kWh for coal and 0.23kgCO2/kWh for natural gas. This doesn't take into account any losses when trying to capture the heat, which would tend to be higher for coal as is harder to capture heat from the smoke stack, so coal emissions are probably heading towards double those of natural gas. It should also be noted that if the heat is used to generate electricity 45-65% of the energy will be lost in the conversion. Electricity is a high grade (low entropy
 ) form of energy, but
that makes it hard to create.
) form of energy, but
that makes it hard to create.For much more data try table 1d on page 10 of the 2012 Guidelines to Defra / DECC's GHG Conversion Factors
 . This and
associated documents considers green house gas equivalents for
additional combustion by-products and includes transport cost too.
. This and
associated documents considers green house gas equivalents for
additional combustion by-products and includes transport cost too.Chemical Fuel
 I am not a chemist but have done some background reading on the
feasibility of using my excess renewable electricity to produce a
chemical fuel. This is a good solution to long term energy storage
because once produced the chemical fuel does not require any additional
energy input during storage. Achieving a workable solution needs
reference to material energy density
I am not a chemist but have done some background reading on the
feasibility of using my excess renewable electricity to produce a
chemical fuel. This is a good solution to long term energy storage
because once produced the chemical fuel does not require any additional
energy input during storage. Achieving a workable solution needs
reference to material energy density 
Hydrogen (H2)
Making hydrogen is easy, in fact I already produce some as a by-product of charging my lead-acid battery. An electrolysis cell could make hydrogen from water easily and at an acceptable efficiency level in a process which is very easy to control. However, hydrogen is difficult to store, it can not be liquefied at room temperature and would therefore require a compressor and expensive pressure vessel or a cryogenic cooler to liquefy it, both of which require energy and complexity. Compressing hydrogen to 70Mpa (10,000psi !) still only achieves a volumetric energy density of 1.5kWh per litre.Methane (CH4) - Propane (C3H8)
Methane is much more complicated to make, but initial research suggests it is possible. It would require hydrogen (from water) and carbon (from CO2, ideally extracted from the atmosphere) and an exotic catalyst and steam process. This might be possible but does not look to be an energy efficient process maybe only yielding 25% of the input energy as methane. For storage it may be easier liquefied methane than hydrogen, but still isn't simple. However, if it is possible to make methane it would seem logical that making propane (C3H8) could follow a similar process and that is easy to liquefy at modest pressure and stored in low cost cylinders.Methanol (CH3OH)
Methanol is a type of alcohol and liquid at room temperature thus making it trivial to store. It is poisonous and can cause irreparable damage to the optic nerve, leading to blindness so must be handled with care. Methanol can be used as the fuel in a fuel-cell to make electricity so would be an excellent candidate if it could be made efficiently. It would need the same feed material as making methane but I have been unable to find a suitable method.If any chemists would like to help I would be very grateful to hear from you.
Thermal Store
Since the objective of interseasonal storage is to make heat for the house in winter, might it be possible to simply store heat? I already have storage heaters in the house to act as a load dump in spring and autumn when the solar PVs (and wind) are generating too much, could a vast storage heater be built to hold a seasons worth of heat? Intuitively, I suspect insulation is going to be a major, possibly insurmountable, problem but let us go through a 'first order A simplified calculation only taking into account the most significant factors.' evaluation process:
Our house has solid walls and therefore is not as well insulated as a modern house. During the cold winter of 2010/11, I estimated our heat demand at circa 20,000kWh. While this is a little profligate, I'll stick with it as we could better insulate the house to reduce demand, but equally we may wish to add an extension, so the two could balance out. I assume that we require space-heating for half of the year, ramping up from autumn and ramping down in spring, with maximum in January/February.
How much energy to store? If the major energy input is a wind turbine which generates all year round it means the heat store only needs a capacity of half the annual usage, so the heat store is to be 10,000kWh. If the charge source was from a much larger solar PV array the heat store would need to be larger because there would be so much less topping up in winter.
A pair of magnetite An iron oxide mineral with 'fairly normal' specific heat capacity of 752J/kg/K, but a high density of 5177kg/m3, giving it a high volumetric thermal capacity of 3.9MJ/m3/K, but not quite as large as a weird molecule called 'water' which has a volumetric thermal capacity of 4.2MJ/m3/K.
storage heater bricks stores 2.7kWh and measure 230 x 190 x 90mm (say 4 litres) including appropriate void for heating element. So, to store 10,000kWh will require 3700 brick-pairs with a volume of 14800 litres. They could be packed into a box 2.5m cubed and weigh around 75 tonnes.
In order to hold 10,000kWh the bricks will be heated to around 650°C and here lies the problem. Insulating the stack sufficiently will be extremely difficult especially considering that a high temperature insulation must be used. For example calcium silicate insulation which will cope with the high temperature has a thermal conductivity
 of 0.063W/m/K (at 200°C), in comparison
polyurethane foam is three times better at 0.021W/m/K but can't take the
high temperature.
of 0.063W/m/K (at 200°C), in comparison
polyurethane foam is three times better at 0.021W/m/K but can't take the
high temperature.Allowing for a thick 0.5m of calcium silicate insulation around our 2.5m cube, which has a surface area of 37.5m2 we find the heat loss when at 650° to be a staggering 3kW, so to maintain its temperature requires 72kWh input per day, or seven times the average output of my solar PV installation. Actually, it is somewhat worse than this because the insulation thickness has increased the surface area to 73.5m2 so the heat loss is even greater.
This quick calculation gives an idea of the magnitude of the problem associated with interseasonal storage. Thermal loss is proportional to temperature difference and also proportional to surface area. If we could store the same energy at a lower temperature the losses will reduce, but unless we can find a material with increased volumetric thermal capacity we will need a larger volume. An increased volume may not be such a bad requirement because the losses due to surface area will go up with the square, whereas the gain in volume goes up with the cube.
There are other methods such as phase change materials which may be worth evaluation, so I may come back to wax later.
One of the best volumetric thermal capacity materials is water at 4.2MJ/m3/K. Since we want to keep the temperature low to minimise the heat loss, this could be a good option. Let us look at how to store 10,000kWh in a water tank:
For simplicity it would easier if there was enough thermal gradient between the tank and house to allow easy heat transfer directly into underfloor heating or large area radiators. We may specify a minimum tank temperature of 35°C, but we will come back to the evaluate the consequence of this decision later. If the maximum water temperature is 85°C we would need 171m3 of water to store the heat energy. That is a lot but not impossibly large. To minimise heat loss we need a tank with minimal surface area, which means a sphere. A spherical tank may be too difficult to construct so perhaps a dumpy cylinder is the most manageable solution.
A storage cylinder 6m diameter and 6m tall could store 170m3 which covers our capacity requirement. Let's have a play around with heat losses: in the depths of winter if the tank was above ground it is possible that the mean external temperature could be 0°C, if it was buried in a (very) big hole it may be 10°C. But what if the tank was inside the house at 20°C? The calculations assume a majority of the insulation uses polyurethane foam giving conductivity of 0.025W/m/K
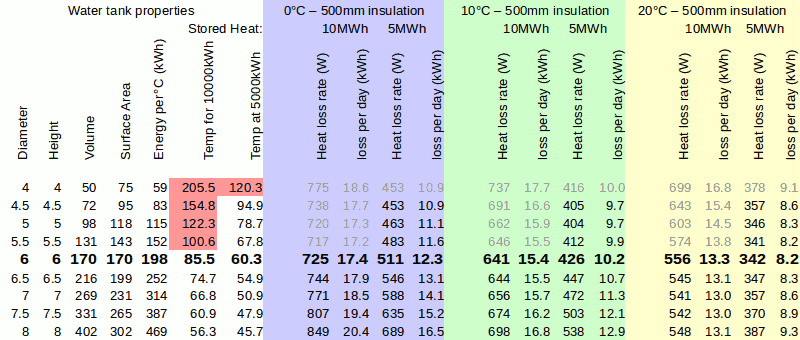
The red area is insufficient to store the required heat because the water will boil, the calculated losses are greyed out. It is interesting to note that when fully charged with heat, bigger sized tanks have lower losses, but as the heat is removed smaller tanks become more efficient. If the tank is inside the building then losses become beneficial in winter since they simply become the heat source for the house, less insulation can be tolerated. However, in summer, pushing heat into the house is a serious problem.
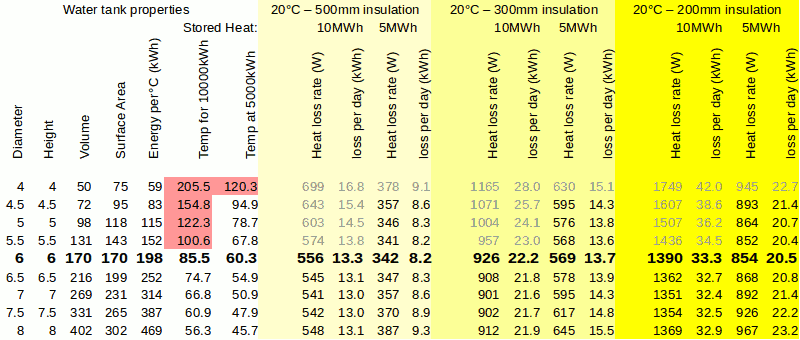
A possible solution to overheating in summer could be to introduce a void between the tank insulation and the building which surrounds it, the unwanted heat would pass into this void could be vented. It would probably need forced air to achieve adequate flow, the vent system would be closed in winter allowing the heat to enter the house. Clearly, less insulation is an advantage - lower cost, smaller overall size, less environmental embedded energy of the system - but it is a compromise. Too little insulation will mean excess heat being vented in summer, maybe so much that insufficient energy is available to overcome the losses and achieve a full heat-charge. Taking account of year-round losses an internal tank with 300mm insulation easily outperforms an external tank with 500mm of insulation. However, the internal 300mm configuration will require a non-trivial 22.2kWh input per day just to maintain the heat charge when it is storing 10,000kWh.
A plan is developing, it is a 'big' solution, with a big cost, but is starting to look do-able.
More evaluation to follow, I'll attempt to model the heat transfer and renewable energy generation requirements. I don't have enough, but since I am generating electricity, the input can be 'boosted' with a heat-pump.



